Du har måske hørt udtrykket "Markov-kæde" før, men medmindre du har taget nogle klasser på sandsynlighedsteori eller datalogi-algoritmer. Sådan lærer du programmering uden al stress Sådan lærer du programmering uden al stress. Måske har du valgt at forfølge programmering, uanset om det er en karriere eller bare som en hobby. Store! Men måske begynder du at føle dig overvældet. Ikke så stor. Her er hjælp til at lette din rejse. Læs mere, du ved sikkert ikke, hvad de er, hvordan de virker, og hvorfor de er så vigtige.
Forestillingen om en Markov-kæde er et "under hood" -koncept, hvilket betyder, at du ikke rigtig behøver at vide, hvad de er for at drage fordel af dem. Du kan dog helt sikkert drage fordel af at forstå, hvordan de virker. De er enkle endnu nyttige på så mange måder.
Så her er et crash kursus - alt hvad du behøver at vide om Markov kæder kondenseret ned i en enkelt, fordøjelig artikel. Hvis du vil dybere endnu dybere, prøv gratis informationsteori kursus på Khan Academy (og overveje andre online kursus websteder også 8 Awesome hjemmesider at tage gratis college kurser online 8 fantastiske hjemmesider til at tage gratis college kurser online læs mere).
Markovkæder 101
Lad os sige, at du vil forudsige, hvordan vejret bliver som i morgen. En sand forudsigelse - den slags udført af eksperte meteorologer 7 Bedste gratis vejrapplikationer til Android 7 Bedste gratis vejrapps til Android Læs mere - ville involvere hundredvis eller endda tusindvis af forskellige variabler, der hele tiden skifter. Vejrsystemerne er utroligt komplekse og umulige at modellere, i hvert fald til lekere som dig og mig. Men vi kan forenkle problemet ved at bruge sandsynlighedsoverslag.
Forestil dig at du havde adgang til tredive års vejrdata. Du starter i begyndelsen og bemærker at dag 1 var solskinnende. Du fortsætter med at bemærke, at dag 2 var også solskinnende, men dag 3 var overskyet, så dag 4 var regnfuld, hvilket førte til tordenvejr på dag 5 efterfulgt af solskins og klar himmel på dag 6.
Ideelt set ville du være mere granulær og vælge en time-by-time analyse i stedet for en dag-til-dag analyse, men dette er kun et eksempel for at illustrere konceptet, så tag med mig!
Du gør dette over hele det 30-årige datasæt (som ville være bare genert af 11.000 dage) og beregne sandsynlighederne for, hvad morgendagens vejr vil være som baseret på dagens vejr. For eksempel, hvis i dag er solrigt, så:
- En 50 procent chance for at i morgen bliver solrig igen.
- En 30 procent chance for at i morgen bliver overskyet.
- En 20 procent chance for at i morgen vil være regnfuldt.
Gentag dette for enhver mulig vejrforhold. Hvis i dag er overskyet, hvad er chancerne for, at i morgen bliver solrigt, regnfuldt, tåget, tordenvejr, hailstorm, tornadoer osv.? Næsten snart har du et helt system af sandsynligheder, som du kan bruge til at forudsige ikke kun morgendagens vejr, men dagens vejr og den næste dag.
Overgangsstater
Dette er essensen af en Markov-kæde. Du har individuelle stater (i dette tilfælde vejrforhold) hvor hver stat kan overgå til andre stater (f.eks. Solrige dage kan overgå til overskyede dage), og disse overgange er baseret på sandsynligheder. Hvis du vil forudsige, hvordan vejret kan være i en uge, kan du undersøge de forskellige sandsynligheder i løbet af de næste syv dage og se, hvilke der er mest sandsynlige. Således en Markov "kæde".
Hvem er Markov? Han var en russisk matematiker, der kom op med hele ideen om en stat, der fører direkte til en anden stat baseret på en vis sandsynlighed, hvor ingen andre faktorer påvirker overgangskancen. Grundlæggende opfandt han Markov-kæden, dermed navngivningen.
Hvordan Markov-kæder anvendes i den virkelige verden
Med forklaringen ud af vejen, lad os undersøge nogle af de rigtige applikationer, hvor de kommer til nytte. Du kan blive overrasket over at finde ud af, at du har brugt Markov-kæder hele tiden uden at vide det!
Navn Generation
Har du nogensinde deltaget i tabletopspil, MMORPG-spil eller endda fiktionskrivning? Du har muligvis forvirret navnene på dine tegn (i det mindste på et eller andet tidspunkt) - og når du bare ikke kunne synes at tænke på et navn, du kan lide, har du sikkert været til en online navnegenerator Opret et nyt alias med The Bedste online-navngeneratorer [Weird & Wonderful Web] Opret et nyt alias med de bedste online-navngeneratorer [Weird & Wonderful Web] Dit navn er kedeligt. Heldigvis kan du gå online og vælge et nyt alias ved hjælp af en af de utallige navne generatorer tilgængelige på Internetz. Læs mere .
Har du nogensinde spekuleret på, hvordan disse generatorer fungerede? Som det viser sig, bruger mange af dem Markov-kæder, hvilket gør det til en af de mest anvendte løsninger. (Der er andre algoritmer derude, der er lige så effektive, selvfølgelig!)
Alt du behøver er en samling breve, hvor hvert brev har en liste over mulige opfølgende bogstaver med sandsynligheder. Så for eksempel bogstavet "M" har en 60 procent chance for at føre til bogstavet "A" og en 40 procent chance for at føre til brevet "I". Gør dette til en hel masse andre bogstaver, og kør algoritmen. Boom, du har et navn, der giver mening! (Det meste af tiden, alligevel.)
Google PageRank
En af de interessante konsekvenser af Markov-kæde-teorien er, at når længden af kæden stiger (dvs. antallet af overgangstal øges), sænker sandsynligheden for at du lander i en bestemt tilstand på et fast nummer, og denne sandsynlighed er uafhængig af hvor du starter i systemet.
Dette er meget interessant, når du tænker på hele verdensomspændingen som et Markov-system, hvor hver webside er en stat, og forbindelserne mellem websider er overgange med sandsynligheder. Denne sætning siger dybest set, at uanset hvilken webside du starter på, er din chance for at lande på en bestemt webside X en fast sandsynlighed, idet du antager en "lang tid" for surfing .
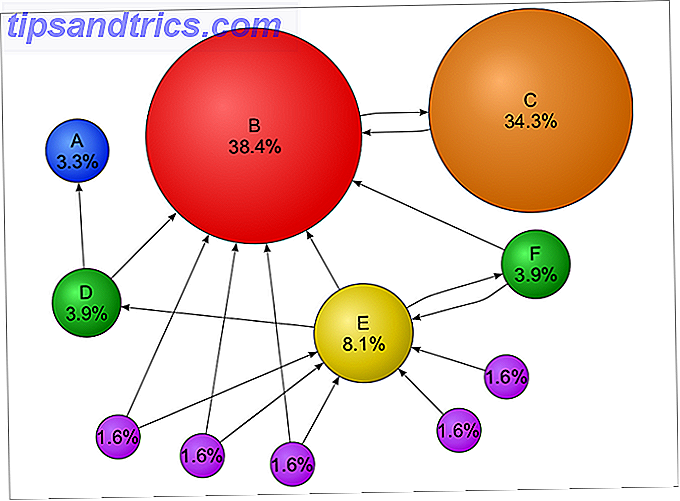
Og dette er grundlaget for, hvordan Google rangerer websider. Faktisk er PageRank-algoritmen en modificeret (læs: mere avanceret) form for Markov-kædealgoritmen.
Jo højere den "faste sandsynlighed" for at komme til en bestemt webside, jo højere er PageRank. Dette skyldes, at en højere fast sandsynlighed indebærer, at websiden har mange indkommende links fra andre websider - og Google antager, at hvis en webside har mange indkommende links, så skal det være værdifuldt. Jo flere indgående links, jo mere værdifulde er det.
Det er mere kompliceret end det selvfølgelig, men det giver mening. Hvorfor får et websted som About.com højere prioritet på søgeresultatsider? Fordi det viser sig, at brugerne har en tendens til at ankomme der, da de surfer på internettet. Interessant, er det ikke?
Skrivning af Word Prediction
Mobiltelefoner har haft prædiktiv skrivning i årtier nu, men kan du gætte hvordan disse forudsigelser bliver lavet? Hvad er det bedste alternative tastatur til Android? Vi kigger på nogle af de bedste tastaturer i Play Butik og sætter dem på prøve. Flere) eller iOS (Alternative tastaturvalg 9 Alternative IOS-tastaturer, der gør din skrivning lettere eller mere sjov 9 Alternative IOS-tastaturer, der gør din skrivning lettere eller mere sjov Når Apple endelig stoppede med at fungere som en overbeskyttet forælder og introducerede tredjeparts tastaturer, gik alle keyboard-crazy. Læs mere), der er en god chance for, at din app vælger Markov-kæder.
Derfor spørger tastaturapplikationer, om de kan indsamle data på dine skrivevaner. I Google Keyboard er der f.eks. En indstilling kaldet Delestykker, der beder om at "dele uddrag af, hvad og hvordan du skriver i Google Apps for at forbedre Google Keyboard". I det væsentlige bliver dine ord analyseret og indarbejdet i appens Markov-kæde sandsynligheder.
Det er derfor, at tastaturapplikationer ofte præsenterer tre eller flere muligheder, typisk i størst sandsynlighed for mindst sandsynlige. Det kan ikke helt sikkert vide, hvad du mente at skrive næste, men det er korrekt oftere end ikke.
Subreddit Simulation
Hvis du aldrig har brugt Reddit, opfordrer vi dig til i det mindste at tjekke dette fascinerende eksperiment kaldet / r / SubredditSimulator.
Simpelthen sætter Subreddit Simulator en massiv del af ALLE kommentarer og titler på tværs af Reddits mange lokalsamfund, og analyserer derefter ord for ord-sminke af hver sætning. Ved hjælp af disse data genererer det ord-til-ord sandsynligheder - bruger derefter disse sandsynligheder til at generere titler og kommentarer fra bunden.
Et interessant lag til dette eksperiment er, at kommentarer og titler kategoriseres af det samfund, hvorfra dataene kom, så de slags kommentarer og titler, der genereres af / r / matets datasæt, er vildt forskellige fra kommentarerne og titlerne genererer ved / r / fodboldens datasæt.
Og den sjoveste - eller måske den mest foruroligende - del af alt dette er, at de genererede kommentarer og titler ofte kan skelnes fra dem, der er lavet af virkelige mennesker. Det er helt fascinerende.
Kender du til andre flotte anvendelser til Markov-kæder? Har du spørgsmål, der stadig skal besvares? Lad os vide i en kommentar nedenunder!